С.Ф. Коваль, В.П. Шаманин  "Растение в опыте"

 

В литературе много раз отмечалось, что изменение физических свойств макромолекул и субклеточных структур - это первая реакция клетки на любое внешнее воздействие [Александров, 1975]. Одно из проявлений этой реакции состоит в изменении полупроницаемости внешней мембраны клетки и увеличении диффузии органических и минеральных веществ во внешнюю среду. Контроль за изменением проницаемости можно вести по выходу из клетки органических веществ при помощи интерферометра или по электрозаряженным ионам, по изменению электропроводности бидистиллированной воды, в которой инкубируется навеска. В силу большей технической простоты, распространение получил второй метод, но все приведенные ниже рассуждения справедливы и для наблюдения за диффузией органических веществ.

Начиная с работы Декстера [Dexter, 1930], определение вымываемости электролитов широко используется для тестирования самых первых реакций клетки на внешнее воздействие [Барашкова и др., 1971; Гужова и др., 1984; Лукатин и др., 1993; Чиркова, 1983]. Мы рассмотрим более подробно этот метод, поскольку на его примере удобно показать некоторые характерные ошибки и порядок осмысливания полученного результата.

Обычно скорость выхода электролитов определяют при помощи реохорного моста по изменению электрического сопротивления за какой- то отрезок времени, и результаты для удобства выражают в обратных омах (1/Ом), т.е. в электропроводности. Последняя молча принимается нами как пропорциональная концентрации электролитов. Если во всех случаях для инкубации использовалось одинаковое количество бидистиллята, то электропроводность последнего будет зависеть от веса навески и исходного количества электролитов в ней.

Поэтому простое сравнение электропроводности для различных образцов некорректно. Более информативно выражение результатов измерения в процентах от суммы электролитов в образце [Коваль, 1974-

б]. Для этого (после проведения измерений) образец убивают замораживанием в жидком азоте или нагревом в той же порции бидистиллята. Затем проводят новое измерение сопротивления, результаты которого соответствуют общей сумме электролитов в образце.

Вторая проблема состоит в введении поправки на неодинаковый вес навесок, поскольку аналитически точное выравнивание их слишком трудоеко. И здесь возникает вопрос о том, в каком соотношении находятся концентрации электролитов и зависящая от них электропроводность.

Для низких концентраций, с которыми мы имеем дело в этом эксперименте, прямая пропорциональность концентрации и электропроводности отмечается не у натуральных величин, а у их логарифмов, в чем легко убедиться, определив электропроводность эксудата убитых листьев при разведении их в 10,100 и 1000 раз (рис 6.7). Точность определения вымываемости по логарифмическому графику в значительной степени зависит от близости фактического tg а к приведенному на рисунке, где tg а = 1. Поэтому при переходе на новые объекты исследования необходимо уточнить значение этого тангенса, измерив сопротивление в шкале разведения эксудатов убитого образца.

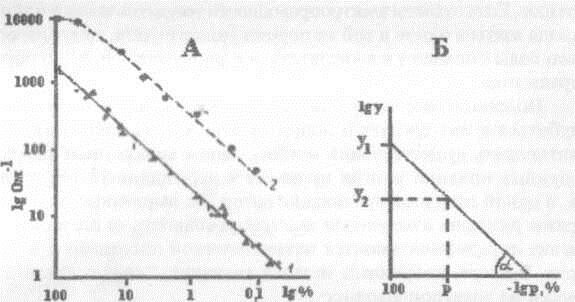
Рис. 6.7. А - изменение электропроводности (lg Ом ') по мере разведения (lg %):

1. - кипяченый экстракт гороха и пшеницы, 2. - 0.1 М раствор NaCl/Б. - логарифмический график, иллюстрирующий вычисление вымытых электролитов (р) по электропроводности эксудата убитого (у,) и живого (у₂) образцов

 

Из уравнения прямой для зависимости log р = f (log у) мы имеем:

In у₂ = a In р + b

где: b = In у₁ - отсчет электропроводности эксудата убитых тканей; In у₂ - отсчет электропроводности живого образца, а=tg а - угол наклона прямой пропорциональности концентрации и электропроводности; р - процент вымытых электролитов. Подставив эти значения, получим:

a In р = In у₂ - In у₁

p^a=e^{(ln y2-ln y1)}

р=(у₂/у₁)^1/a

или для частного случая угол а равен 45°:

Р=У₂/У₁

Таким образом, процент вымытых электролитов может быть определен как отношение электропроводности эксудата испытуемого образца к электропроводности эксудата, убитого в степени 1/а. Ошибка, возникающая в связи с отклонением знаменателя в показателе степени от 1,0, не является постоянной величиной. С увеличением процента вымываемости ошибка резко возрастает, но при работе с однородными объектами и при различии вымываемости в пределах одного порядка она не существенна. Здесь же решается и проблема выравнивания измеряемых образцов. Если отсчеты электропроводности эксудатов живого и убитого образца взяты в одной и той же порции бидистиллята, то вес навески и объем воды попадают и в числитель, и в знаменатель и таким образом сокращаются.

Подобные рассуждения всегда выполняет создатель методики, но углубиться в них следует и пользователю. Очень часто приходится адаптировать существующий метод к своим конкретным задачам, а бездумные новации иногда приводят к неожиданным результатам. Так, в одной солидной публикации автор для выравнивания размеров образца разделил измеренную электропроводность на вес навески. Но деление логарифмов является математической операцией извлечения корня. В итоге, получилась нелепая величина: “корень степени веса навески из электропроводности”.

Измерение динамики выхода электролитов может дать дополнительную ценную информацию. На рисунке 6.8 приведены результаты измерения выхода электролитов из листьев пшеницы. Быстрый выход электролитов в первые 40-60 минут инкубации сменяется далее более слабым, но стабильным в течение следующих трех часов. Кривая суммарного выхода состоит из двух последовательно соединенных ветвей, каждая из которых в некотором приближении представляется прямой линией с плавным переходом между ними. Следовательно, мы имеем дело с двумя различными процессами. У пораженного экологическим стрессом образца возрастает не только угол наклона первой ветви к горизонтальной оси, но и соответствующий угол второй ветви.

Первая ветвь характеризует выход электролитов из кажущегося свободного пространства [Коваль, 1974-6], в котором ионы перемещаются в соответствии с законами диффузии и адсорбции. Вторая, с меньшим углом наклона, отражает в чистом виде функциональную активность плазмалеммы, ее сопротивление диффузионнму проникновению

 

электролитов, когда концентрация в свободном пространстве становится близкой к нулю. Концентрация электролитов в свободном пространстве определяется равновесием диффузии из клетки и обратным закачиванием их против градиента концентраций, которое может происходить только с затратами энергии. Логичным объяснением пониженного поглощения ионов и связанного с этим роста их концентрации в свободном пространстве будет предположение о дефиците АТФ, необходимого для принудительного транспорта против градиента концентраций.

Следовательно, если отсчет электропроводности эксудата взят после короткой экспозиции (до 40 минут), он отражает не выход электролитов через плазмалемму, а их концентрацию в кажущемся свободным пространстве. Она зависит от обратной закачки в клетку (против градиента концентраций) ионов, диффундирующих в свободное пространство.

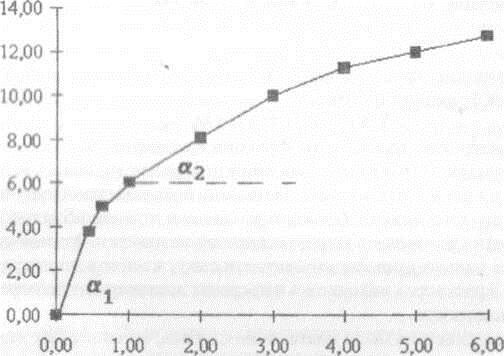
Рис. 6.8. Динамика вымываемости электролитов из листа пшеницы.

Угол а, отражает скорость выхода ионов из кажущегося свободного пространства, угол а₂ - проницаемость мембраны клетки. Для получения характеристики проницаемости плазмалеммы в чистом виде нужно взять  разность между процентами вышедших электролитов после одного и после двух часов инкубации и выразить как процент от общей суммы электролитов в клетке.